５．実験開始

実験開始まで来ました

伝達関数の計測
　今回の計測点数は９点



データ基準点
　加振点は、全てのモードの腹（振幅があり、節ではない点）に近い 点、このケースではフリーフリーの条件のため、�@、�B、�F、�Hは節にならない。　今回�@を基準点とします。

計測する伝達関数の数
今回�@を基準点（固定点）とすると、伝達関数は、�@−�@、�@−�A…�@−�Hの組み合わせで９個あります。

データ計測方法
　データの計測で�@を基準点とすると、以下の方法があります
　・　�@を 加振して、応答のセンサーを�@から�Hまで移動する方法（これが標準）
　・　�@に応答のセンサーを取り付け、加振を�@から�Hま で移動する方法
　但し今回の鉄板に関しては線形として問題ないため、加振点移動でもＯＫ

計測開始
　以下のように伝達関数を計測する
コヒーレンスは値が０から１の関数で、伝達関数の信頼性を示しています。コヒーレンスの値 が１に近い周波数は、伝達関数の信頼性が高く、０に近い周波数は 信頼性は良くありません。
                     
                         　　伝達関数                                                   コヒーレンス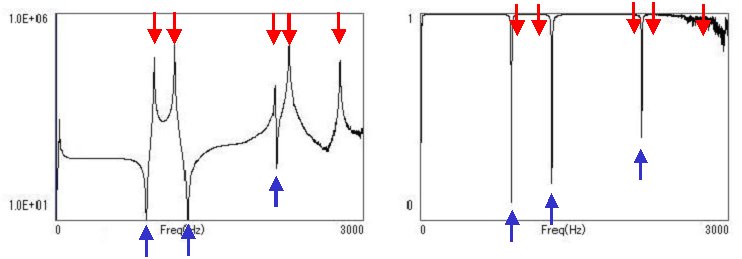


上記の図は、コヒーレンスがほとんどの周波数において、１に近い値であり、伝達関数の信頼性は良いことがわかります。特に伝達関数のピーク周波数において コヒーレンスの値が１に近い事が重要です（赤い矢印）
但し、伝達関数の谷に当たる周波数（青い矢印）は加振を行っても応答がない周波数であり、これは信号のS/Nのため、コヒーレンスが小さい値でも問題あり ません。
伝達関数計測中は、時間データ、伝達関数、コヒーレンス等に気をつけながら加振を行います

また、1箇所の伝達関数を計測ごとにデータを保存しますが、加振位置と応答位置の情報も一緒に指定して保存します。例えば、ポイント１のＺ方向の場合は、 １Ｚと指定します。